元論文のリンク
Introduction
multi labelのlearningにもPU使えますよね?あるデータxに対して、複数の属性がある(タグ付けみたいに)時がmulti label learning。
この論文の問題設定は以下の3つ。
- サンプル xにたいして、絶対にpositiveであるラベルがある。
- サンプル xに対して、そのラベルは付けされいないが、絶対に含まれないというわけではないラベルがもう1つ。
- サンプル xは複数個のラベルが付きうる。
これをPUに帰着するとき、multi label PU ranking問題にしている。
Related Work
label rankingベースの研究がメイン。これはすべてのpositive例をnegative例の上に順位付けするという問題設定で、損失はRank Lossなるものであり先行研究でも提案されている。WSABIEとか。
Multi-label Ranking
問題設定。
- Xはサンプル空間であり、 xはサンプル。
- ラベルは合計で m種類あり、 Y={0,1}mである。1は付いていて、0は付いてない。
- 与えられたデータセットは S={(xi,yi)}i=1Nである。
- 訓練する識別器は f(x)=(f1(x),⋯,fm(x))Tである。各ラベルについてつくかつかないかを予測する。
- 目標としては、以下のように、損失を最小限に抑えること。
argminfL(f)=Ex,y[L(f(x),y)] そして、ここではRank Lossを使う。
Rank Loss
Lrank(f(x),y)=∑i,j:yi=1,yj=0[[fi(x)<fj(x)]]+21[[fi(x)=fj(x)]] [[⋅]]演算は指示関数で、条件を満たすならば1となる。
Ranking関数について、今回は0と1の二値しかないので上のような形になっている。すべての大小関係がはっきりしているペアについて、順序がひっくり返っているならペナルティ1、同じ順序なら0.5のペナルティを足すかたち。
これを用いて式変形すると、
argminfL(f)=Ex,y[L(f(x),y)]=∑y∈Yp(Y)Ex∣y[Lrank(f(x),y)]=∑y∈Yp(Y)∑i,j:yi=1,yj=0Ex∣y[[[fi(x)<fj(x)]]+21[[fi(x)=fj(x)]]] この期待値の部分はmiss rank rateというものであり、以下のように書き直すこともできる。
R(x,i,j)=Ex∣y[[[fi(x)<fj(x)]]+21[[fi(x)=fj(x)]]]=Ex∣yi=1,yj=0[[[fi(x)<fj(x)]]+21[[fi(x)=fj(x)]]]=p(fi(x)<fj(x)∣yi=1,yj=0)+21p(fi(x)=fj(x)∣yi=1,yj=0) これを使って書き直せば、以下のように損失関数になる。
Lrank(x,y)=∑i,j:yi=1,yj=0p(yi=1,yj=0)R(x,i,j)=∑1≤i<j≤mp(yi=1,yj=0)R(x,i,j)+p(yi=0,yj=1)p(x,j,i) i<jという条件を付けてループを回せば、このように「iは正しくjは違う確率」と「iは違いjは正しい確率」の和を考えている不整合を2つ分加算すればよく、計算が楽にできる。
この研究のシナリオはCase-Control。
Multi-label PU ranking
前述のように、multi-label PU rankingは以下の2つのラベルの状況から学習するものであった。
- サンプル xにたいして、明確にラベルが割り当てられている場合、それはPositiveと見なせる。
- ラベルが割り当てられてない場合、必ずNegativeではないとは限らない。Unlabeledとみなせる。
cost sensitiveなPU Learningへの帰着
上の式に cij,cjiという、クラスiがクラスjに誤分類された時のペナルティの重みを付ける。論文
例によって、 R(x,i,j)も p(yi=1,yj=0)なども、Negativeデータがないので計算できない。これをPUで計算するために以下のような新たな誤分類率? RX(x,i,j)を定義する。
RX(x,i,j)=p(fi(x)<fj(x)∣si=1,sj=0)+21p(fi(x)=fj(x)∣si=1,sj=0) ラベルがついているか、ついていないかの sで判断する。ここでのsはPN分類で与えられたラベルyの代わりであるPUのラベル。
これを不適切そうだが、割り切って使うとして、損失関数を新たに書き換えてみると以下のようになる。
L^rank(x)=∑1≤i,j≤mp(si=1,sj=0)RX(x,i,j)+p(si=0,sj=1)RX(x,j,i) 仮定はSCAR、Select Completely At Randomで選択される。つまり、p(yi=1∣si=0)=p(yi=1)である(選ばれるかどうかと関係なしにラベルがつく確率は同じ)
そして、p(x∣si=1)=p(x∣yi=1)、PUの時のラベル付きは、PNの時のPositiveサンプルと同じような分布が得られるというのもSCAR仮定からわかる。
2014 du Plessisらの書き換えと同様に、 RXは以下のように書き換えできる。
πj∣i=p(yj=1∣yi=1)R−X(x,i,j)=p(fi(x)<fj(x)∣yi=1,yj=1)+21p(fi(x)=fj(x)∣yi=1,yj=1) - πj∣iはi番目の属性がPositiveであるときの、j番目もPositiveである確率。
- R−Xは、足していく値は RXと同じだが、 yi=1,yj=1という前提条件としている。
- RXはyではなくsが条件であったし、そのうえsi=1,sj=0という条件であった。
- yi=1という条件付きの下で、 yjについて全パターンを集めて、 πj∣i=p(yj=1∣yi=1)の割合でそれぞれ配分している。
このように、RX,R−Xを定義されたら以下のように、📄 2014-NIPS-[Ramp]Analysis of Learning from Positive and Unlabeled Data, 📄
2014-NIPS-[Ramp]Analysis of Learning from Positive and Unlabeled Data, 📄 2015-ICML-[uPU] Convex Formulation for Learning from Positive and Unlabeled Data で提案されたRXの分解をすることができる。
2015-ICML-[uPU] Convex Formulation for Learning from Positive and Unlabeled Data で提案されたRXの分解をすることができる。
RX(x,i,j)=(1−πj∣i)R(x,i,j)+πj∣iR−X(x,i,j) 2014で提案していた RXの構成を、 yi=1という前提条件の下でやってみたというかたち。
- πj∣iの割合のyi=1∣yj=1の条件の下での損失
- 1−π割合のyi=0∣yj=1の条件の下での損失
つまり、RXというPUで使わないといけない損失は、上のようにPNで計算できる形に分解できる。これをうまく使って、PNの式出てて来る右辺を左辺で置き換えたい。
次のように R(x,i,j)について上の式を解くと、以下のが得られる。を式変形できる。
R(x,i,j)=1−πj∣i1(RX(x,i,j)−πj∣iR−X(x,i,j)) これを用いて、集計を行うと以下のようになる。R−X(x,i,j)+R−X(x,j,i)=1を使う。
結果として、以下の
Lrank(x)=∑1≤i,j≤m{p(yi=1)RX(x,i,j)+p(yj=1)RX(x,j,i)−p(yi=1,yj=1)} が目標関数として得られる。p(yi=1)のClass Priorは事前に得られる。p(yi=1,yj=1)は各クラス間に依存関係がないなら、単純に確率の積で求まるし、あってもLabeledされたデータから推定すればいい。
対称的な損失関数
Lrank(x,y)=∑i,j:yi=1,yj=0p(yi=1,yj=0)R(i,j)=∑1≤i<j≤mp(yi=1,yj=0)R(i,j)+p(yi=0,yj=1)R(j,i) この式を RXに書き換えることによって、以下の形となる。
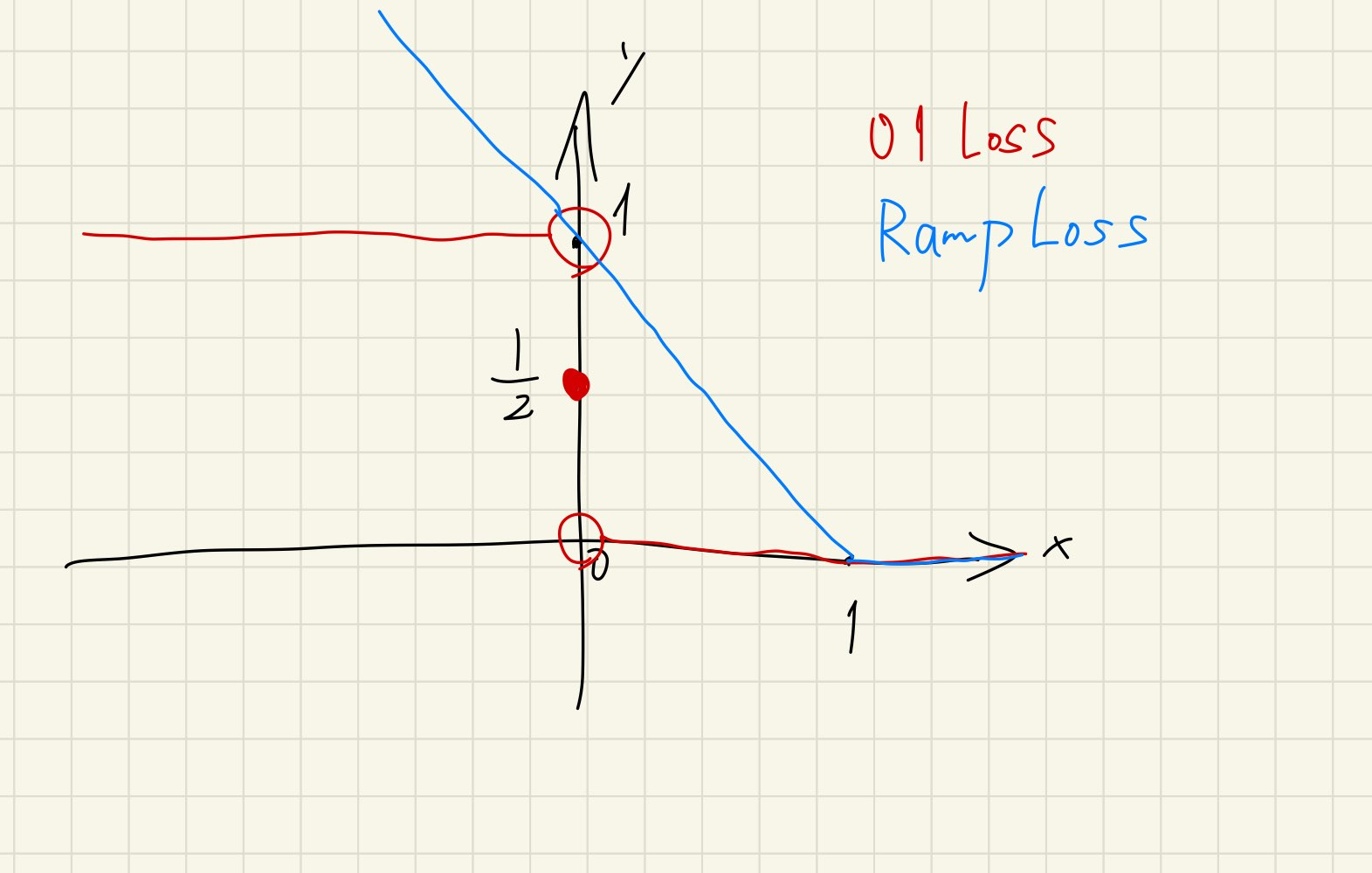
01損失では最適化できないので、代理損失を使うことを考える。
📄 2014-NIPS-[Ramp]Analysis of Learning from Positive and Unlabeled Data で提案していた l(x)+l(−x)=1となる対称な損失関数を、ここでも使うことができる。
2014-NIPS-[Ramp]Analysis of Learning from Positive and Unlabeled Data で提案していた l(x)+l(−x)=1となる対称な損失関数を、ここでも使うことができる。
ここでは、2014 du Plessisの提案にあるように、ランプ損失を使う。多クラス分類版としては、以下のものとなっている。多クラスの分類器の引いた差をRamp損失にそのまま突っ込んでいる。
グラフにしてみると以下のような形
Experiments
使用したデータセットは以下の3つ。
具体的な内容はここをみる。
Settings
ground truthがpositiveのラベルの欠損率を0から80%までで試した。
実験自体は、Single-Training-Set、Select Completely At Randomの設定で行っている。Case-Controlでもできるのでは…?
- 割合から乗算して欠損数を得る。
- 各クラスごとに何個欠けるのかについて、多項分布に従った1つのパターンをランダムに選ぶ。
- 各クラスで何個欠損するのかが決まったので、あとはSCARで選ぶ。
識別器の実装は
f(x)=WTx とこのように多次元SVMであり、optimizationは無印の勾配降下法でやった。
多次元SVMの説明はこちら: 📄 NNDL 第3章 線形学習
NNDL 第3章 線形学習
この上で、L2正則化も行った。
Synthetic Dataset
- 各データについて、n個のラベルが付くとして、これをポアソン分布から得る。
- n個のラベルについてそれぞれ、クラス cを選ぶ確率自体を、多項分布に従い選ぶ。
- そのデータについて、特徴のサンプル回数k自体もポアソン分布から得る。
- 特徴のサンプル回数は、各クラスがそれぞれ特徴を持つとして、それの表現をサンプリング?
- k回のサンプリングをそれぞれ行い、その得た特徴の和をサンプルとしている。
2000のテスト、8000の訓練データ。
実験結果として、全体のクラス数が2と少ないなら、ラベル付きが多ければ多いほど、手法がいい性能を持つが情報が減ると下がる。ただし8まで増えてしまうとなれば性能が低くなる。 全データでののべラベル数/クラス数の割合が性能の重要な鍵だとわかった。
Image Annotation Dataset
画像のデータセット2つ日してベンチマークを行った。訓練済み7層のAlexNetを使った。
Discussion
使用した損失関数と理想的な01損失の損失関数によるRiskの差は、
- p(s=0∣y=1)の項目
- ラベルのペア内の両方のラベルが割り当てられる確率(原文ままこれなに?)に比例する。
また、SCARの設定で問題を解いたので、Case Controlに適用させるとやはり、欠損率が低くても性能が低下する。
提案手法はラベルの欠損率が2割以上の時に有用である。
また、ラベルの存在自体にバイアスがあるとき、例えば犬、猫、人間は高確率で一緒に存在するならば、「猫、人間」、「犬、猫、人間」とラベル付けされたデータは似た特徴を持つかもしれない(というかそもそも同じかもしれない)このようなデータの分離はさすがにこの手法では無理。
クラス事前確率の π=p(y=+1)は雑に推定したが実用上はもっと丁寧に推定するべきだな。
2014-NIPS-[Ramp]Analysis of Learning from Positive and Unlabeled Data, 📄
2015-ICML-[uPU] Convex Formulation for Learning from Positive and Unlabeled Data で提案されたの分解をすることができる。

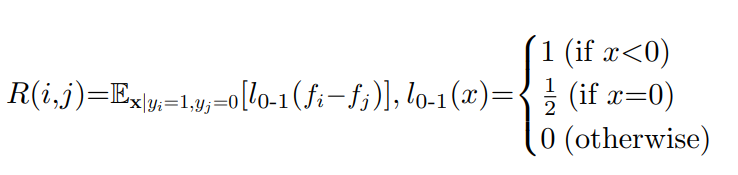
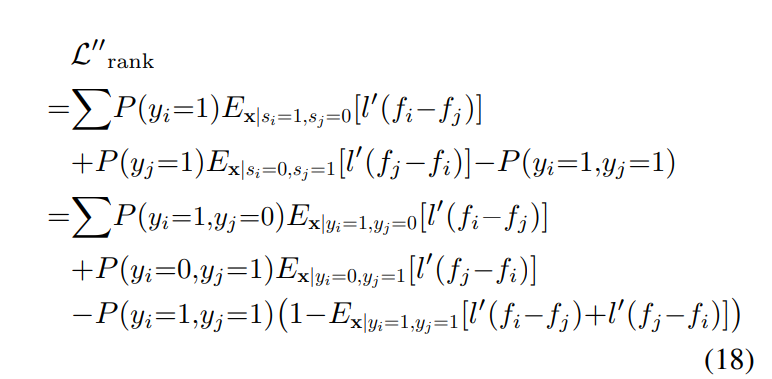
2014-NIPS-[Ramp]Analysis of Learning from Positive and Unlabeled Data で提案していた となる対称な損失関数を、ここでも使うことができる。
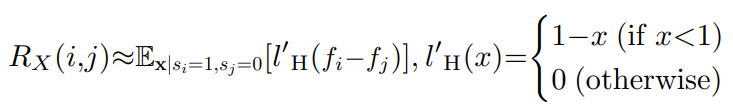
NNDL 第3章 線形学習
